1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 Table of contents

Page 9: 1975, Degree in Mathematics at the University of Amiens. Then Maths teacher in Arras, France.


Adjunct Professor of Mathematics in Arras. It was awful. Absolutely Awful.
Fortunately I still had my second passion, Photography.
I decided to go for a change in culture and in language.
Another scattering of odd jobs across Europe. Then…

Topology is a branch of mathematics
In mathematics, topology is concerned with the properties of space that are preserved under continuous deformations, such as stretching, crumpling and bending, but not tearing or gluing.






Albert Einstein "School failed me, and I failed the school. School bored me. The teachers behaved like Feldwebel (sergeants). I wanted to learn what I wanted to know, but they wanted me to learn for the exam.
Albert Einstein "L'école m'a loupé, et j'ai échoué à l'école. L'école m'ennuyait. Les professeurs se comportaient comme des Feldwebel (sergents). Je voulais apprendre ce que je voulais savoir, mais ils voulaient que j'apprenne pour l'examen.


Then the Rolleiflex Single-Lens, 120 format (the negatives measured 6x6cm), of very good quality, but it had some parallax issues due to the 2 lenses and difficult to focus in low light conditions.
Here I am in Grenoble to take photos at my brother Dominique’s wedding.
Puis le Rolleiflex mono objectif, format 120 (les négatifs font 6x6 cm), très bonne qualité, mais problème de parallaxe dû aux 2 objectifs et mise au point difficile en basse lumière.



PROBLEMS WITH THE FRENCH EDUCATIONAL SYSTEM

In France, here is how, and probably like you, I learned trigonometry, around 1970 in Arras in the Pas-de-Calais: - "Take your notebooks, definition: The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side. To be learned by heart for next week ". Not funny.

In about 1972-75 I learned a lot from talking to math students I met when I was working for the National Trust in England. They know how to motivate their students. See below for trigonometry with Eratosthenes.

As soon as I became a math teacher, I applied the English methods. The principal called me regularly to his office:
- "Mr. Fournier, I passed in the corridor during your class and your pupils were laughing! It's unacceptable, math is serious, coefficient 4 on the BEPC!"
Nowadays, I would slap him and say:
- "My poor sir, you don't know anything about pedagogy or about children. You learn much better when you're relaxed than terrified!"
At that time, there was no training for teachers. For the French National Education, it was enough to know your subject, and presto, you became a teacher, without any advice, without educational training or internship. Well done, you idiots.
It is not because we are good at Maths that we are able to teach it! Most of my teachers weren't. Most of my colleagues weren't either.
When I saw that not only the principal, but also all my colleagues in mathematics and physics were against any innovation, I realized that a career with these idiots for 40 years would not make me happy.
The weight of the French administration sickens me and the pedagogy is ridiculous.
So I quit my teaching post after 4 months, without filling out any papers or saying goodbye.

See also below for mere examples of how poor the French educational system was.

Eratosthenes calculated the circumference of the Earth in the third century BC. It is an extraordinary tale: Eratosthenes (276-194BC) was a geographer, mathematician, and director of the library of Alexandria.
He had heard travelers say that in Syene, at noon on June 21st, you could see the image of the sun reflected in the bottom of a well. This meant of course that the Sun was precisely vertically above the well.
So on June 21st, at noon in Alexandria, Eratosthenes measured the length of the shadow of one of the city’s obelisks.
The Greeks had already figured out that the world was round, for they were great navigators, often in armadas, and they had remarked that when a boat disappeared over the horizon, it was always the prow that disappeared first, no matter where or in what direction they were traveling. From the Atlantic to the Black Sea, the same thing happened, and only a sphere could explain it. They had also understood that a lunar eclipse happened when the Earth’s shadow was projected onto the moon and that this shadow was circular. They had even understood that the sun’s rays, crossing such a far distance, were parallel.
Which allowed him to draw up the following diagram :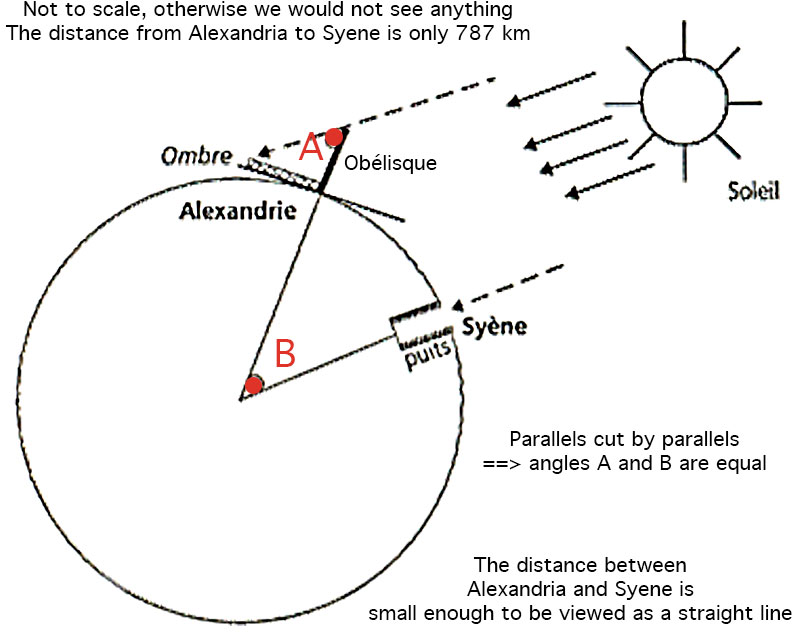



Angles A and B are equal as they are interior angles. So that gives him the angle and the opposite side of an isosceles triangle. Far from being an idiot, Eratosthenes knew that he only needed to calculate the two unknown sides, in this case, the SUN’S RADII! As you well may know, a triangle has only 6 variables: 3 sides and 3 angles. It is evident that once you have 3 of those variables, you can find them all. If you have an angle and two sides, your triangle is well-defined. So there must be calculations that would let you find the other variables. He was right, and so he invented “Trigonometry”.
Eratosthenes was able to find the length of the Earth’s circumference: 39,375km which isn’t too far off. Pretty good job for 300BC.
Bravo, Eratosthenes. Thanks to you, we can learn this so-called Trigonometry. Hurray!
I learned all of these motivating stories by talking to other math students I met while working for the National Trust.
« We have known the radius of Earth since the time of the Greek mathematician and geographer Eratosthenes, about 240 BC. Every year at noon on June 21, the Sun passed directly overhead at Syene, Egypt. Eratosthenes knew this fact. At that same moment, he measured the Sun to be 7.2° off vertical in Alexandria, which is directly north of Syene. Aristotle had argued that Earth, no matter what its orientation, always casts a circular shadow on the Moon during an eclipse of the Moon. The only object that always casts a circular shadow is a sphere; thus, Eratosthenes knew that Earth must be a sphere. He also understood that the 7.2° shift in the altitude of the Sun, as measured from the two cities at the same time, was due to the curvature of Earth’s surface, meaning that the two cities were separated by 7.2° of latitude, or about 1/50 of Earth’s entire 360° circumference. Hire someone to pace off the distance from Alexandria to Syene, multiply by 50, and you have the circumference of Earth—about 25,000 miles. Divide by 2π and you have the radius. It was easy, once someone figured out how to do it! » (de « Welcome to the Universe: An Astrophysical Tour » par Neil deGrasse Tyson, Michael A. Strauss, J. Richard Gott)

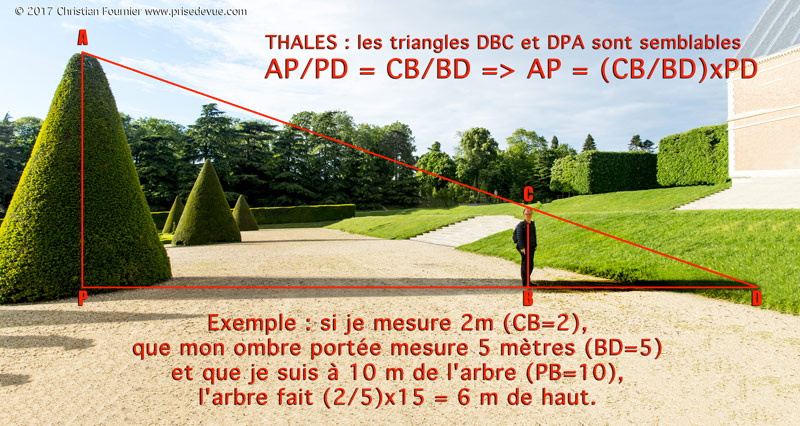
Thales’s theorem.

Legend has it that Thales of Miletus (about 626-547 BC) was invited by King Amasis, warned of his great knowledge. The king declared that he did not know the height of the fantastic pyramids already almost two thousand years old. Thales planted his cane at noon in the sand vertically and said to the king:
"The shadow of my cane is exactly equal to its height, and so must your pyramid." ....
In geometry, Thales's theorem, or intercept theorem, states that on a plane, a line parallel to one of the sides of the triangle cuts it into two similar triangles.

The lines AP and BC are parallel so the triangles DBC and DPA are similar and the sides AP, PD, AD are proportional to the sides BC, BD, and CD. As we can measure the lines PD, BC, CB and BD, we can calculate AP. Magic? No, Mathematics. Bravo, Thales.



At the Parc de Sceaux, I take this opportunity to illustrate my simplified version of Thalès' theorem.
I position myself so that my shadow ends at the same place as that of the tree.



Do you think it’s gotten any better today?


I must not laugh
I must not laugh
I must not laugh

.....




When I saw that not only the principal but all my colleagues in mathematics and physics were against all innovations, I understood that a career with these idiots for 40 years would not make me happy.

Other examples of the French national education of that time:

Program of history in 3rd: the French revolution of 1789. Program of history in second: the French revolution of 1789.
The 14-18 war or the Russian revolution: not a word!

The same teacher of English from second to final, Mr. Taquet: for three years, we have never pronounced a single word of English !!!
I learned English with very good teachers: John, Paul, George and Ringo.






For two years (Math Sup and Math Spé), the word math teacher spoke only with the gifted class, ignoring the other 40 students. The physics teacher said he was against the theory of relativity and did not teach it. I learned everything myself.

My college was named "Lycée Robespierre" after the famous French revolutionary guy. I think this name is inappropriate.

Other examples of the lack of pedagogy in France schools.

Aviation
I got my Private Pilot License (FAA) in the USA in 1982. Why Missouri? Because they offer the course of about one month in all inclusive package, accommodation, meals, theoretical and practical courses, administrative papers and you do not leave school until your diploma is in your pocket.
So they know how to teach effectively. I meet exceptional teachers who know that we learn better by being relaxed than stressed (the opposite of my "superiors" from Arras high school!).
My instructor made me do a full day of "touch and go" (small take-off-landing circuits) while talking to me about other things, then he got out of the plane under the pretext of going to get his cigarettes and told to continue all the same.
I found myself solo, without any apprehension, but of course this instructor "reappeared" by radio contact.
My friend Claude Slowick from the university of Amiens had passed his license in France and told me that, for him, his instructors had spoken to him 6 weeks before about the many dangers and the enormous difficulty of the 1st solo flight. He has not slept the 4 days preceding his solo. Long live US pedagogy!


SCUBA DIVING

I got my first diving diploma in 1980 with Miami Police Chief Diving Instructor Bruce Garrisson, a great guy. He just told me, put your bottle on your back, your mask on your nose and come with me, follow me close and we will have fun. No apprehension, just magnificent, a new world, colorful fish everywhere, a state of weightlessness, total footing.
I of course followed closely my instructor, who did not intend to let go of me an inch (they do not speak in centimeters there).
My first word, once back on land, was: - "where can I buy a Nikonos." I was addicted. Then I took my Padi Open Water course and learned about the dangers and how to avoid them. Then I passed all my diplomas up to Nitrox. Much later, in 1994, after my forced return to France, I got a job thanks to Mrs. Redford, (yes, Robert's wife!), To go and photograph his capsized racing boat off Guadeloupe.
The aim was to photograph the sailboat underwater to show whether its mast was broken or not, which was very important for insurance companies. If the mast is not broken, we straighten ou the boat; if it is broken, we sink it, because only the mast justifies the expense.
So I take the plane with the incomparable Francis Ronat who is in charge of the underwater salvation work.
The Breguet reconnaissance plane responsible for locating the wreckage is late, Francis and I therefore have free time, our diving equipment (except bottles, prohibited in commercial planes) and my Nikonos underwater camera and we decide to go diving as touristes in the Cousteau reserve.
The local diving clubs refuse to give us air because we do not have the diploma of the FFESSM, the French equivalent of Padi.
Unbelivable, Francis (who has been a professional diver for 10 years, he pours concrete under water and repairs the pipes of La Hague, among others) and I have a thousand dives to our credit, professional diplomas recognized around the world, except in France.
We are turned away!
Back in Paris, I therefore take this scuba class.
There I saw the beginners, harnessed with their wetsuit, stab, and depth gauge sitting on the edge of the small pool of 1 meter deep.
The very young instructor then describes to them all the dangers of diving (pulmonary embolism, intoxication of the depths, blocked regulators, exploding bottles), etc. I saw the legs of some of these newbies shake before they faced that leap of death. Long live US pedagogy!

SWIMMING

I learned to swim (very badly) in Arras, France around 1970. The teacher made us do the breaststroke movements on the edge of the pool, hundreds of times, until we did them perfectly. Then he yelled at us because we were unable to do them once in the water. Our fear of water obviously confused us.
I attended swimming lessons in Los Angeles: the instructor played ball with the kids in the pool for hours. Laughs, screams, it's a complete heckling. Nothing is happening, the French said. Serious error! After a while, the teacher loses his watch at the bottom of the water. 10 kids spontaneously dive to get it. Two hours later these kids can swim impeccably. They had learned not to be afraid of water anymore. The rest is just technical details. Long live US pedagogy!






"I will not bow, I will not go away in silence, I will not submit, I will not turn back, I will not conform, I will not shut up.
Courage is to seek the truth and to say it; it is not to suffer the law of triumphant lies." Jean Jaurès.


I don't "believe" in science.
Science works, whether I believe in it or not.



Science teaches us to think rationally.


Il est bien impossible que la constellation Orion, si petite dans le ciel, puisse se refléter sur les pyramides.


I build a model of the caravel, the Pinta, one of the three Christopher Columbus ships, during his trip to "America".
The other boats were called: Niña and Santa María.
Christopher Columbus' father would have had sufficient financial means to send him to the University of Pavia where he studied, in particular, cosmography, astrology and geometry.
Like me, and I went to America too.
Well, I learn that when other people take a picture of me, I am very often blurry.

Learning maths and physics helps to see the difference between the rational and the irrational.



Ignorance leads to fear, fear leads to hatred, hatred leads to violence.

France loses a good teacher, England gains a great photographer.

I decided to go for a change of culture and language. Again I worked some odd jobs across Europe: volunteer work cleaning up the rubble after an earthquake in Monteaperta di Friuli, near Udine, Italy; photographer for Club Med in Corfou, Greece; photographer/videographer for Butlin’s Holidays Ltd, Bognor Regis Sussex (we had to ask the guests to pay for their photo before taking it! Club Med and cruiseships were easy after that!); salesman/demonstrator for Electrosonic slide projectors in London, I went to Norway to see Ina who I met at Friday Bridge, etc…


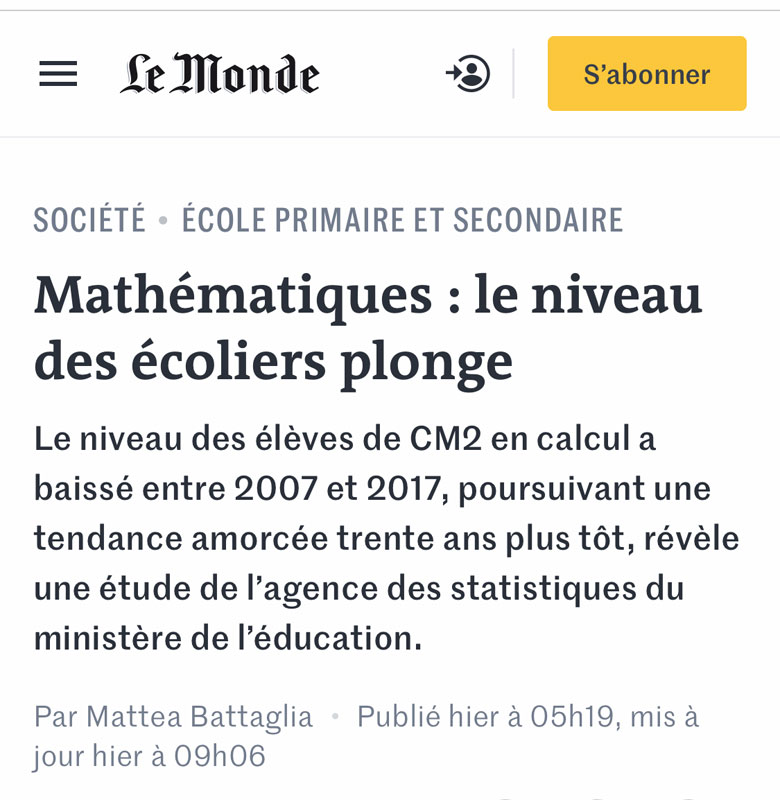
If I had not dropped everything to get into photography, I would have become a maths teacher, and then I would have killed myself.



Maths and science levels in school: French chilldren are the worst of all Europe in 2020.
Math teacher in France: an endangered profession (2015) Les performances en mathématiques des élèves en France, aussi bien au primaire que dans le secondaire. Dans les deux cas, le niveau global est en sérieuse baisse. La situation au primaire est encore plus inquiétante. Dans la dernière étude internationale (TIMSS) qui évaluait le niveau en mathématiques des élèves de CM1, on trouvait la France en dernière position du classement avec un score moyen de 488 points quand la moyenne européenne était de 527 points. Ce résultat est très loin de la perception que l’on peut avoir du niveau en mathématiques de notre pays, il devient donc urgent d’agir pour inverser cette tendance. Le problème en France n’est pas celui de la « quantité » mais bien celui de la « qualité » d’enseignement. C’est d’ailleurs sur cet aspect qualitatif que la situation devient particulièrement préoccupante. Les difficultés en mathématiques ne se cantonnent pas aux élèves, le mal est plus profond et concerne aussi nos enseignants. Ainsi, les connaissances en mathématiques de ceux qui exercent dans le premier degré (en maternelle et au primaire) sont insuffisantes quand une crise de vocation touche certaines académies du second degré (collège et lycée). Sur le premier degré, ce constat n’est pas surprenant quand on sait que plus de 80% des étudiants qui se prédestinent à devenir professeur des écoles sont titulaires d’une licence en Lettres, Arts ou Sciences Humaines. Ils ont, pour un grand nombre d’entre eux, en héritage de leur scolarité antérieure, des difficultés, voire une aversion, envers les mathématiques. Ainsi, toujours selon l’étude TIMSS, les enseignants du primaire en France sont moins nombreux à déclarer se sentir à l’aise ou très à l’aise lorsqu’il s’agit d’améliorer la compréhension des mathématiques des élèves en difficulté (61 % contre 79 % en moyenne). Il en est de même lorsqu’il s’agit d’aider les élèves à comprendre l’importance des mathématiques (70 % contre 88 % en moyenne) ou de donner du sens aux mathématiques (72 % contre 85 % en moyenne) (voir la note de la DEPP du ministère de l’éducation pour davantage d’informations). Les étudiants sont moins nombreux à vouloir devenir prof de math que par le passé. En conséquence, certains postes restent vacants depuis quelques années, notamment pour aller exercer dans les secteurs les plus défavorisés. Cette pénurie d’enseignants nuit aux élèves qui en ont le plus besoin mais ne peut être considérée comme surprenante, tant les salaires en début et en milieu de carrière manquent d’attractivité en France. Le niveau en mathématiques de nos élèves est en baisse depuis plus d’une décennie. Les solutions sont pourtant nombreuses pour enrayer cette spirale. Il sera important de mettre l’enseignement des mathématiques au cœur d’une réflexion plus globale sur le métier d’enseignant, au risque de voir la chute se poursuivre. Cette entrée a été publiée dans Education, avec comme mot(s)–clef(s) éducation, enseignants, mathématiques, OCDE, PISA.







Nous vivons dans une société extrêmement dépendante de la science et de la technologie, dans laquelle presque personne ne comprend la science et de la technologie.
"It is better to aim for perfection and miss it than to aim for mediocrity and reach it." Francis Blanche

I’m fully aware that my letters were far lousy in the beginning. I’m a numbers guy, not a words guy! And, well, I wasn’t the best typist on my second-hand Remington. Don’t worry, over time I get much better and I become a decent journalist, combining my pen with my pictures. I am particularly proud of my article on Haiti (page 23), my description of my work on cruise liners (page 19, at the end) and my report on my ruin, written on the verge of suicide (page 41, at the end).



Raphaël Christian Fournier at the residence of M et Mme Courcelle, 22 rue Charles Dubois 80 000 Amiens, February 23 1975.
First, « See you Soon » doesn’t necessarily mean within 20 days. I don’t have a lawyer. I hope you’re doing well… in health, in your studies, emotionally, and all those other things you need to do “well”.
Thank you for your letter, it’s true I haven’t got much free time, I have too much on the go and it’s wearing me down (math, Beaux-Arts, English, Photo club organizer, 10 hours of math tutoring per week to eke out a living, it doesn’t sound like a lot but it is, skating, etc. etc. It all eats up quite a lot of my time. I still manage to somehow mess up my sensitive paper with my photo boxes. I’ve just successfully written my exam for the unit on topology and less successfully the one for algebra.
Why am I in Amiens? For the coffee machine. It is a magnificent machine: SILENCE, precision, efficiency, a part in an erotic slot. A part rings, a button pressed, a soft hum, and it’s ready. It was love at first sight, blinding love at first sight, I signed up without hesitation. You might be thinking that the lid has flipped on this coffee machine, but that’s only because you haven’t got a sentimental coffee machine that doesn’t want to suffer anymore and who knows that it’ll suffer if it gets too attached.
And how are things with you? Where do you live? What are you doing? I am going back to work with the National Trust in the forest for 15 days at Easter in Britain.
I’ve enclosed a photo of my specter seen through a window in Brighton. Your friend, Raphaël Christian Fournier

Here I meet Angelo Falcone, second from the right.

And Christian Parramon.
Who I met again over the years. Here in 2014 in Fontainebleau. In the background, Frédérique Gosky


"Peter Adams: Photography is not about cameras, gadgets and gismos.
Photography is about photographers.
A camera does not make a great picture any more than a typerwriter writes a great novel."

My art work: Leaves in a stream in Peak District, UK.
As ever my photos, more or less abstract. Here, some dead leaves at the bottom of a creek. ART.

At the university in Amiens I met Michère Giry, of whom I haven’t a single photo (yes, it does happen!). She could have been the French Joan Baez, but, contrary to me, she chose to go for her Agrégation (competitive exam allowing you to teach at the secondary and post-secondary level in France) and became a teacher…


SUNDAY
I took a shower this morning
And I took my time, too,
As it was Sunday, a rare thing.
What I saw in the mirror plunged me
Into profound reflection.
My wet hair flattened,
My wet bear straightened.
Is there a difference in nature between
These two capillary systems?
A short hair straightens when wet,
A long hair flattens when wet,
Or maybe : Am I just under the weather?
Night is now falling
It was a gloomy Sunday
And the meanderings of my brain have grown tired
After such meandering the whole day.
And I feel quite depressed and worried,
To remain silent
Before this important problem,
This hairy problem,
Bare yet prickly :
Am I under the weather?

Poem (in case it wasn’t obvious) by Christian Fournier. Sad that the main joke doesn’t translate well! “Problème à poil” means “Hair problem” but also “Naked problem”

If you were wondering, the answer to the question is yes.




If you are born in Israel, you are probably Jewish.
If you are born in Saudi Arabia, you are probably Muslim.
If you are born in India, you are probably Hindu.
If you are born in North America, you are probably Christian.
Your faith is not inspired by a divine truth, it's just geography.

Patriotism is your belief that this country is superior to all others, because you were born there.








In order to understand the universe, you must know the language in which it is written and that language in mathematics.




Je ne garde pas ce que je pêche. J'enfonce un hameçon dans son visage, je l'extirpe de l'eau, j'arrache l'hameçon, et je le rejette, le laissant se demander pourquoi Dieu autorise une telle chose.


The imposture of science education in French high schools, by Bertrand Rungaldier
Posted on June 25, 2013

Depuis leur invention il y a environ 2500 ans, les mathématiques passent pour la discipline de déduction par excellence. Si Platon avait inscrit au fronton de l'Académie "Nul n'entre ici s'il n'est géomètre" ce n'était pas parce qu'il exigeait de savoir faire des constructions compliquées à la règle et au compas mais bien parce qu'il demandait à ses élèves de savoir mener un raisonnement et d'avoir un esprit critique envers leurs propres affirmations.

Si 2000 ans plus tard Pascal louait "l'esprit de finesse et de géométrie" c'était pour la même raison : acquérir de la méthode, savoir analyser un problème, savoir le scinder en problèmes plus petits, les résoudre rigoureusement, faire la synthèse du tout. Et ce n'est pas un hasard si à la même époque, Descartes inventait la géométrie analytique dans un essai intitulé "Règles pour la direction de l'esprit" et non un traité de géométrie ou de mathématiques. Partout, en Grèce ou en France, toujours, dans l'antiquité ou à l'époque moderne, les mathématiques ont constitué la discipline de référence en matière de raisonnement.

Il est évident que cette façon de procéder, cette démarche intellectuelle que nous nommons désormais "scientifique" peut s'appliquer à n'importe quelle discipline intellectuelle; l'immense avantage des mathématiques est qu'il est extrêmement facile de savoir si l'on a bien conduit son raisonnement ou si l'on a correctement effectué son calcul tout simplement parce que chaque étape dudit raisonnement est clairement identifiée. Il est infiniment plus simple de savoir si l'on a correctement effectué un calcul ou si l'on a effectivement prouvé tel théorème que de savoir si l'on a correctement traduit un sonnet de Shakespeare, un poème de Goethe ou une page des Frères Karamazov.

Les Mathématiques ont pour fonction de former à l'art du raisonnement et à la méthode scientifique. C'est là leur essence et c'est ce qui les distingue de l'art du calcul pratiqué par les Egyptiens ou les babyloniens.

Il apparaît malheureusement que cette fonction primordiale ait été totalement oubliée par les rédacteurs des récents et actuels programmes d'enseignements des Mathématiques en lycée. On peut même se demander dans quelle mesure ils n'ont pas tout simplement décidé que désormais les Mathématiques ne devaient plus former à la rigueur et au raisonnement tant les programmes de lycée ont été véritablement exterminés au cours de ces dernières années.







Diana Frances Spencer, née le 1ᵉʳ juillet 1961 à Sandringham et morte le 31 août 1997 à Paris, est une aristocrate anglaise, membre de la famille royale britannique. Elle épouse en 1981 Charles, prince de Galles, avec qui elle a deux enfants : William, en 1982, et Henry, en 1984
Sur mes cahiers d’écolier Sur mon pupitre et les arbres Sur le sable de neige J’écris ton nom
Sur toutes les pages lues Sur toutes les pages blanches Pierre sang papier ou cendre J’écris ton nom
Sur les images dorées Sur les armes des guerriers Sur la couronne des rois J’écris ton nom Sur la jungle et le désert Sur les nids sur les genêts Sur l’écho de mon enfance J’écris ton nom
Sur les merveilles des nuits Sur le pain blanc des journées Sur les saisons fiancées J’écris ton nom
........
Sur mes refuges détruits ... Et par le pouvoir d’un mot Je recommence ma vie Je suis né pour te connaître Pour te nommer Liberté Paul Eluard, Poésies et vérités, 1942


My favorite scientists

I photographed 10 great scientists


1 - Christian Deduve, prix Nobel de médecine
2 - Pr Thaisa, Storchi Bergmann, chercheuse en astrophysique
3 - Claude Allègre, géochimiste, prix Crafoord et médaillé du CNRS
4 - Christian Chabrol, a réalisé la première greffe cardiaque en Europe
5 - Robert Clark, National Geographic photographer
6 - Hubert Reeves, chercheur en astrophysique
7 - Thomas Pesquet, spationaute ISS
8 - Claudie Haignère, spationaute Soyouz
9 - Pierre-Gilles de Gennes, prix Nobel de physique
10 - Michel Cymes, médecin français, chirurgien connu pour ses activités d'animateur de télévision et de radio

Il manque le Dr Jean-Louis Étienne, voir plus bas



My super-heros :



1927 Solvay Congress Conference on Electrons and Photons
Congrès Solvay sur les Electrons et Photons, à l'Institut international de physique Solvay dans le parc Léopold à Bruxelles. (Dix-sept des vingt-neuf personnalités présentes sont lauréates d'un prix Nobel.)


Rangée à l'arrière / back :

Auguste Piccard, Émile Henriot, Paul Ehrenfest, Édouard Herzen, Théophile de Donder, Erwin Schrödinger,
Jules-Émile Verschaffelt, Wolfgang Pauli, Werner Heisenberg, Ralph H. Fowler, Léon Brillouin;
Rangée du milieu / middle :

Peter Debye, Martin Knudsen, William Lawrence Bragg, Hendrik Anthony Kramers,
Paul Dirac, Arthur Compton, Louis de Broglie, Max Born, Niels Bohr;
Rangée à l'avant / front :

Irving Langmuir, Max Planck, Marie Curie, Hendrik Lorentz, Albert Einstein, Paul Langevin,
Charles-Eugène Guye, Charles Thomson Rees Wilson, Owen Willans Richardson.





Carl Sagan





Carl Sagan (1934 – 1996) est un scientifique et astronome américain. Il est l'un des fondateurs de l'exobiologie. Il a mis en place le programme SETI de recherche d'intelligence extraterrestre. Il est aussi renommé pour son scepticisme.

Carl Sagan était professeur et directeur de laboratoire à l'Université Cornell et a contribué à la plupart des missions automatiques d'exploration spatiale du système solaire.

Il est également connu pour avoir coécrit un article annonçant les dangers de l'hiver nucléaire.
Pendant la première guerre du Golfe, Sagan a prédit que la fumée engendrée par les bombardements américains des puits et raffineries de pétrole irakiens entraînerait des conséquences proches de l'hiver nucléaire.

Sagan est surtout connu du grand public pour ses œuvres de vulgarisation scientifique. Il a écrit et raconté la série télévisée Cosmos (treize épisodes vus par 10 millions de téléspectateurs) dans laquelle il développe, entre autres, un calendrier cosmique. Celui-ci sera souvent repris par la suite dans plusieurs livres et documentaires de vulgarisation de l'astronomie.

Sagan fut l'un des pères fondateurs d'un des groupes sceptiques américains, le Committee for Skeptical Inquiry, qui considère qu'aucune preuve de l'existence du paranormal n'a été apportée à ce jour. Son ouvrage The Demon-Haunted World est considéré comme un classique du scepticisme scientifique.


Le plus incroyable, c'est qu'il soit complétement inconnu en France, bien qu'ayant quasiment sauvé la planète d'une guerre nucléaire en rencontrant Ronald Regan et Gorbatchev à l'époque de la guerre froide et l'accumulation inconsidérée de bombes atomiques dans chaque camp et leur expliquant qu'ils étaient comme deux guerriers dans un garage inondé d'essence et se menaçant chacun avec une boîte d'allumettes.

En prenant l’avion de Los Angeles à Paris, quand je suis retourné en France en 1992, j’ai vécu le même phénomène de science-fiction que dans le film "Yesterday" ou tout d’un coup les Beatles n'ont jamais existés, avec le scientifique Carl Sagan. En France il n'avait jamais existé !





"Nous vivons dans une société dépendante des sciences et technologies dans laquelle presque personne ne connait les sciences et technologies."





The sad truth is that you learn more about ASTRONOMY through the internet or self-study than you do at school.



Le fait qu'il existe 14 seasons de la série Kardashians et seulement deux de la série Cosmos de Carl Sagan résume bien l'Humanité.




Comprendre est une sorte d'ectase.


La science nous apprend à penser rationnellement


Il nous avait prévenu en 1995 ...



« Vulgariser la science - essayer de rendre ses méthodes et ses découvertes accessibles à des non-scientifiques - me vient naturellement et immédiatement. Ne pas expliquer la science me semble pervers. Quand tu es amoureux, tu veux le dire au monde.
Ce livre est une déclaration personnelle, reflétant ma longue histoire d'amour avec la science. Mais il existe une autre raison: la science est plus qu’un corpus de connaissances, c'est une façon de penser.
J’ai l'horrible vision d’une Amérique pour mes enfants ou de mes petits-enfants :
- Les États-Unis deviennent une économie de services et d’information,
- Presque toutes les industries manufacturières clés se sont envolées vers d'autres pays
- Des pouvoirs technologiques impressionnants sont entre les mains de très peu de personnes et que personne, représentant l’intérêt public, ne peut même saisir les problèmes,
- Quand les gens ont perdu la capacité d'établir leurs propres agendas ou de poser des questions en connaissance de cause à ceux qui détiennent l'autorité
- Quand, contemplant nos boules de cristal et consultant nerveusement nos horoscopes, nos facultés critiques en déclin, incapables de faire la différence entre ce qui est bon et ce qui est vrai, nous glissons, presque sans nous en rendre compte, dans la superstition et l’obscurité. »

(De « Le monde hanté par les démons: la science comme une bougie dans le noir (Edition anglaise) » par Carl Sagan en 1995)



Excerpt from Cosmos by Carl Sagan 1980:
The Sphinx, half human, half lion, was constructed more than 5,500 years ago. Its face was once crisp and cleanly rendered. It is now softened and blurred by thousands of years of Egyptian desert sandblasting and by occasional rains. In New York City there is an obelisk called Cleopatra's Needle, which came from Egypt. In only about a hundred years in that city's Central Park, its inscriptions have been almost totally obliterated, because of smog and industrial pollution—chemical erosion like that in the atmosphere of Venus. Erosion on Earth slowly wipes out information, but because they are gradual—the patter of a raindrop, the sting of a sand grain—those processes can be missed. Big structures, such as mountain ranges, survive tens of millions of years; smaller impact craters, perhaps a hundred thousand; and largescale human artifacts only some thousands. In addition to such slow and uniform erosion, destruction also occurs through catastrophes large and small. The Sphinx is missing a nose. Someone shot it off in a moment of idle desecration—some say it was Mameluke Turks, others, Napoleonic soldiers. On Venus, on Earth and elsewhere in the solar system, there is evidence for catastrophic destruction, tempered or overwhelmed by slower, more uniform processes: on the Earth, for example, rainfall, coursing into rivulets, streams and rivers of running water, creating huge alluvial basins; on Mars, the remnants of ancient rivers, perhaps arising from beneath the ground; on Io, a moon of Jupiter, what seem to be broad channels made by flowing liquid sulfur. There are mighty weather systems on the Earth—and in the high atmosphere of Venus and on Jupiter. There are sandstorms on the Earth and on Mars; lightning on Jupiter and Venus and Earth. Volcanoes inject debris into the atmospheres of the Earth and Io. Internal geological processes slowly deform the surfaces of Venus, Mars, Ganymede and Europa, as well as Earth. Glaciers, proverbial for their slowness, produce major reworkings of landscapes on the Earth and probably also on Mars. These processes need not be constant in time. Most of Europe was once covered with ice. A few million years ago, the present site of the city of Chicago was buried under three kilometers of frost. On Mars, and elsewhere in the solar system, we see features that could not be produced today, landscapes carved hundreds of millions or billions of years ago when the planetary climate was probably very different.
There is an additional factor that can alter the landscape and the climate of Earth: intelligent life, able to make major environmental changes. Like Venus, the Earth also has a greenhouse effect due to its carbon dioxide and water vapor. The global temperature of the Earth would be below the freezing point of water if not for the greenhouse effect. It keeps the oceans liquid and life possible. A little greenhouse is a good thing. Like Venus, the Earth also has about 90 atmospheres of carbon dioxide; but it resides in the crust as limestone and other carbonates, not in the atmosphere. If the Earth were moved only a little closer to the Sun, the temperature would increase slightly. This would drive some of the CO2 out of the surface rocks, generating a stronger greenhouse effect, which would in turn incrementally heat the surface further. A hotter surface would vaporize still more carbonates into CO2, and there would be the possibility of a runaway greenhouse effect to very high temperatures. This is just what we think happened in the early history of Venus, because of Venus' proximity to the Sun. The surface environment of Venus is a warning: something disastrous can happen to a planet rather like our own.
The principal energy sources of our present industrial civilization are the so-called fossil fuels. We burn wood and oil, coal and natural gas, and, in the process, release waste gases, principally CO2, into the air. Consequently, the carbon dioxide content of the Earth's atmosphere is increasing dramatically. The possibility of a runaway greenhouse effect suggests that we have to be careful: Even a one- or two- degree rise in the global temperature can have catastrophic consequences. In the burning of coal and oil and gasoline, we are also putting sulfuric acid into the atmosphere. Like Venus, our stratosphere even now has a substantial mist of tiny sulfuric acid droplets. Our major cities are polluted with noxious molecules. We do not understand the long- term effects of our course of action.
But we have also been perturbing the climate in the opposite sense. For hundreds of thousands of years human beings have been burning and cutting down forests and encouraging domestic animals to graze on and destroy grasslands. Slash-and-burn agriculture, industrial tropical deforestation and overgrazing are rampant today. But forests are darker than grasslands, and grasslands are darker than deserts. As a consequence, the amount of sunlight that is absorbed by the ground has been declining, and by changes in the land use we are lowering the surface temperature of our planet. Might this cooling increase the size of the polar ice cap, which, because it is bright, will reflect still more sunlight from the Earth, further cooling the planet, driving a runaway albedo (1) effect?
Our lovely blue planet, the Earth, is the only home we know. Venus is too hot. Mars is too cold. But the Earth is just right, a heaven for humans. After all, we evolved here. But our congenial climate may be unstable. We are perturbing our poor planet in serious and contradictory ways. Is there any danger of driving the environment of the Earth toward the planetary Hell of Venus or the global ice age of Mars? The simple answer is that nobody knows. The study of the global climate, the comparison of the Earth with other worlds, are subjects in their earliest stages of development. They are fields that are poorly and grudgingly funded. In our ignorance, we continue to push and pull, to pollute the atmosphere and brighten the land, oblivious of the fact that the long-term consequences are largely unknown. A few million years ago, when human beings first evolved on Earth, it was already a middle-aged world, 4.6 billion years along from the catastrophes and impetuosities of its youth. But we humans now represent a new and perhaps decisive factor. Our intelligence and our technology have given us the power to affect the climate. How will we use this power? Are we willing to tolerate ignorance and complacency in matters that affect the entire human family? Do we value short-term advantages above the welfare of the Earth? Or will we think on longer time scales, with concern for our children and our grandchildren, to understand and protect the complex life-support systems of our planet? The Earth is a tiny and fragile world. It needs to be cherished. 1. The albedo is the fraction of the sunlight striking a planet that is reflected back to space. The albedo of the Earth is some 30 to 35 percent. The rest of the sunlight is absorbed by the ground and is responsible for the average surface temperature.
Copyright © 1980 by Carl Sagan Productions, Inc. Excerpted by permission of Ballantine Books, a division of Random House LLC. All rights reserved. No part of this excerpt may be reproduced or reprinted without permission in writing from the publisher.


« Right now the doubling time of the world population is about 40 years. Every 40 years there will be twice as many of us. As the English clergyman Thomas Malthus pointed out in 1798, a population increasing exponentially—Malthus described it as a geometrical progression—will outstrip any conceivable increase in food supply. No Green Revolution, no hydroponics, no making the deserts bloom can beat an exponential population growth. » (de « Billions & Billions: Thoughts on Life and Death at the Brink of the Millennium » par Carl Sagan)

Circa 1985 « Today, the United States and the Soviet Union have booby-trapped our planet with almost 60,000 nuclear weapons. Sixty thousand nuclear weapons! Even a small fraction of the strategic arsenals could without question annihilate the two contending superpowers, probably destroy the global civilization, and possibly render the human species extinct. No nation, no man should have such power. We distribute these instruments of apocalypse all over our fragile world, and justify it on the grounds that it has made us safe. We have made a fool’s bargain. » (de « Billions & Billions: Thoughts on Life and Death at the Brink of the Millennium » par Carl Sagan)








"The warming up of our planet is a chain reaction: heat generated by humans create CO2 which rises in the atmosphere. The CO2 in the atmosphere then warms the planet like a coat which makes the CO2 rise in the atmosphere, and warms up the planet, and so on. Carl Sagan* warned us in 1985. He calculated that if humans do not act on it immediately (1985), due the chain reaction, in 30 years time (2015), it will be too late to reverse the reaction. When the young people of today (2023) in France demonstrate for their retirement at 60, or 62 or 64, they are wrong: since nobody cares about global warming, the world will already be unlivable by then." Christian Fournier.

Carl Sagan, great astronomer, science popularizer and science fiction writer, one of the greatest of the 20th century, passed away on December 20, 1996, at the age of only 62.
Her great passion for astronomy as a life teacher continues to amaze even today all over the earth.
He was one of the founders of the SETI project, for the search for extraterrestrial intelligence.
He was a pioneer of exobiology and NASA consultant for the most important planetary space missions.
He wrote Dragons of Eden, Considerations on the Evolution of Human Intelligence, which won the Pulitzer Prize, and the science fiction novel Contact, which was followed by the film with Jodie Foster, which won the Hugo Prize.
He and Frank Drake, on the Pioneer 10 probe en route since 1972, affixed the famous plaque bearing the peace greeting of a naked man and woman, representatives of mankind, to any extraterrestrial intelligence.
Thanks to him, on the two Voyager satellites launched on 1977, a gold gramophone record travels in space, the Voyager Golden Record, with sounds and images of the different varieties of life and culture on Earth.
Sagan and the commission put together 115 images and many natural sounds: those produced by waves, wind, thunder, animal sounds, birds and whales singing.
Music from different cultures and eras was included, and greetings from the inhabitants of the Earth in 55 different languages.
Carl Sagan is the author of one of the most beautiful reflections on astronomy and life of all time, when he observed the earth, our home, as a pale blue dot, taken up at his request by Voyager 1, in 1990, already 6 billion km away from the earth.
Among the many writings of humanity, Carl Sagan's reflections on Pale Blue Dot occupy a special place in the heart of every astronomer and every lover of the starry sky.
The Pale Blue Dot in the photo is less than a pixel large, and indicates with disconcerting clarity the smallness of our position in the boundless Universe.
Here are Carl Sagan's moving and unforgettable reflections:
From this distant vantage point, the Earth might not seem of any particular interest.
But for us, it's different.
Look again at that dot.
That's here.
That's home.
That's us.

On it veryone you love, everyone you know, everyone you ever heard of, every human being who ever was, lived out their lives.
The aggregate of our joy and suffering, thousands of confident religions, ideologies, and economic doctrines, every hunter and forager, every hero and coward, every creator and destroyer of civilization, every king and peasant, every young couple in love, every mother and father, hopeful child, inventor and explorer, every teacher of morals, every corrupt politician, every "superstar," every "supreme leader," every saint and sinner in the history of our species lived there -- on a mote of dust suspended in a sunbeam.
The Earth is a very small stage in a vast cosmic arena.
Think of the rivers of blood spilled by all those generals and emperors so that, in glory and triumph, they could become the momentary masters of a fraction of a dot.
Think of the endless cruelties visited by the inhabitants of one corner of this pixel on the scarcely distinguishable inhabitants of some other corner, how frequent their misunderstandings, how eager they are to kill one another, how fervent their hatreds.
Our posturings, our imagined self-importance, the delusion that we have some privileged position in the Universe, are challenged by this point of pale light.
Our planet is a lonely speck in the great enveloping cosmic dark.
In our obscurity, in all this vastness, there is no hint that help will come from elsewhere to save us from ourselves.
The Earth is the only world known so far to harbor life.
There is nowhere else, at least in the near future, to which our species could migrate.
Visit, yes. Settle, not yet.
Like it or not, for the moment the Earth is where we make our stand.
It has been said that astronomy is a humbling and character-building experience.
There is perhaps no better demonstration of the folly of human conceits than this distant image of our tiny world.
To me, it underscores our responsibility to deal more kindly with one another, and to preserve and cherish the pale blue dot, the only home we've ever known.
Carl Sagan
Pale Blue Dot
"We are the local embodiment of a Cosmos grown to self-awareness.
We have begun to contemplate our origins: starstuff pondering the stars"

Carl Sagan in 1985:
Thanks very much. Senator [David] Durenberger, Senator [Al] Gore, Senator [Quentin] Burdick, I’m glad to be here. As I understand, my function is to give some sense of what the greenhouse effect is, to try to say something about the greenhouse effect on other planets, and to again underscore that this is a real phenomenon. And then perhaps I can take the liberty to say a few remarks about what to do about it.
The power of human beings to affect control and change the environment is growing as our technology grows, and at the present time, we clearly have reached the stage where we are capable, both intentionally and inadvertently, to make significant changes in the global climate and in the global ecosystem. And we’ve probably been doing on a smaller scale things like that for a very long period of time. For example, slash and burn agriculture, which has been with us for tens of thousands of years, probably, changes the climate to some extent by changing the albedo, the reflectivity of the Earth.
That massive changes have occurred is clear from the historical record. For example, Egypt was once the breadbasket of the Roman Empire. It may be the same role as the American Midwest plays today. That is certainly no longer the case. It’s not a greenhouse effect issue. It may be an overgrazing issue, but it is an example of how humans are perfectly capable of making these unexpected and inadvertent changes.
Because the effects occupy more than a human generation, there is a tendency to say that they are not our problem. Of course, then they are nobody’s problem, not on my tour of duty, not on my term of office. It’s something for the next century. Let the next century worry about it. But the problem is that there are effects, and the greenhouse effect is one of them which have long time constants. If you don’t worry about it now, it’s too late later on. And so in this issue, as in so many other issues, we are passing on extremely grave problems for our children when the time to solve the problems, if they can be solved at all, is now.
If you ask, what determines the Earth’s climate? Clearly, the main thing that determines it is sunlight. Sunlight is what heats the Earth. Not all the light that arrives at the Earth from the Sun goes to heating the Earth. Some of it is reflected back. It’s just the part that is absorbed and what happens is there’s a certain rate at which sunlight is absorbed by the Earth’s surface. And there’s a certain rate at which the Earth’s surface radiates to space.
What comes from the Sun is in the ordinary visible part of the spectrum that our eyes are sensitive to. What the Earth radiates into space is in the infrared part of the spectrum. Longer waves than red that our eyes are not sensitive to. But it’s as legitimate, a form of light as the kind that we’re used to.
Now, if you calculate what the temperature of the Earth ought to be from how much sunlight is being absorbed, equaling how much infrared radiation would be radiated to space, you find that the Earth’s temperature, by this simple calculation, is too low. It’s about 30 centigrade degrees, too low. And why is it too low? It’s too low because something was left out of the calculation. What was left out of the calculation? The greenhouse effect.
The air between us is transparent, except in Los Angeles and places of that sort. In the ordinary visible part of the spectrum, we can see each other. But if our eyes were sensitive at, say, 15 microns in the infrared, we could not see each other. The air would be black between us. And that’s because, in this case, carbon dioxide. Carbon dioxide is very strongly absorbing at 15 microns. And other wavelengths in the infrared. Likewise, there are parts of the infrared spectrum where water vapour absorbs, where we could not see each other if we were only as far apart as we are in this room.
If you add these infrared absorbing gases to a planet, then what happens is the sunlight comes in as before. But when the surface tries to radiate the space in the infrared, it is blocked. It is impeded by the absorbing gasses. And so, the surface temperature has to rise so that there is an equilibrium between what comes in and what goes out. So this is the greenhouse effect. It is a misnomer for more reasons than one. It’s a misnomer in particular because that’s not how a florist greenhouse works, but that’s a very minor point.
There are other gases which absorb in the infrared, all of them, many of which have been mentioned already,: nitrous oxide, methane, the halocarbons. And these are products partly of agriculture. It’s fertilizers, refrigeration, aerosol spray cans, and so on, all products of our technology. We don’t generate much water into the atmosphere, but we certainly do generate a great deal of carbon dioxide through the burning of wood and fossil fuels and apparently benign activity. Who could object to humans burning oil and coal, gas and wood?
I’d like to stress that the greenhouse effect makes life on Earth possible. If there were not a greenhouse effect, the temperature would, as I say, be 30 centigrade degrees or so colder. And that’s well below the freezing point of water everywhere on the planet. The oceans would be solid after a while.
A little greenhouse effect is a good thing, but there is a delicate balance of these invisible gases, and too much or too little greenhouse effect can mean too high or too low a temperature. And here we are pouring enormous quantities of CO2 and these other gasses into the atmosphere every year, with hardly any concern about its long-term and global consequences.
Now, certainly, not all aspects of how increased CO2 and other gasses into the atmosphere affect the climate are known. There are still many uncertainties, although the overall picture is, I think, quite clear and quite widely understood and accepted.
But there are questions about aerosols and about clouds. You heat up the Earth. How much increase or decrease in cloudiness is there? How does that change the albedo or reflectivity of the Earth? There’s questions about the ocean and its response time to an increase in CO2. There are feedback effects, and therefore it is certainly worthwhile to spend some additional money on further research on the subject.
Another point is that the significant temperature changes on the Earth between ice ages and out of ice ages, glacial and interglacial time periods, seem to be connected with quite small changes in the amount of sunlight that reaches the Earth due to changes in the Earth’s orbital properties. And that is a suggestion that the Earth’s climate system may be very delicately dependent on the sorts of factors that we’re talking about here. And that’s why it makes sense to study past climatic changes on the Earth in an attempt to obtain some calibration.
Another source of calibration is the other planets. Every planet with an atmosphere has some degree of a greenhouse effect. The most spectacular case by far is the greenhouse effect of Venus. It’s the nearest planet about the same mass-radius density as the Earth. But it is spectacularly different in several respects, one of which is that the surface temperature is about 470 degrees centigrade, 900 fahrenheit. And that enormous temperature is not due to it being closer to the Sun, because Venus is surrounded by bright clouds, and, in fact, because it reflects so much light back to space, if that’s all that was happening, it would be cooler, not warmer than the Earth.
The reason for this absurdly high temperature on the surface of Venus, which is well understood, I mean, Soviet spacecrafts have landed on Venus and, in effect, stuck out a thermometer. There’s no doubt that the surface temperature is very high, and later U.S. spacecrafts have as well. The reason is a massive greenhouse effect in which carbon dioxide plays a major role.
Now, the amount of CO2 in the Venus atmosphere is much larger than here. The atmosphere is almost entirely carbon dioxide, and there’s 90 times more of it there than here. But it is an indication of what can happen in an extreme case.
You look at Mars or Jupiter or Titan, the big moon of Saturn, and you have additional examples of greenhouse effects, different gases, different amounts of sunlight reaching the surface, different planetary albedoes and cloudiness. And in all those cases, there is also a greenhouse effect.
In addition, it has been possible to calculate those greenhouse effects fairly accurately, so that the kind of theoretical armamentarium which is used to calculate the greenhouse effect. Greenhouse effect changes on the Earth is also used for other planets and therefore can be calibrated to some extent against those other planets. If we keep coming up with the right answer in all those different cases, we probably understand fairly well how greenhouse effects work.
It would, however, be worthwhile along the lines that Senator Gore was talking about to have an increased program through NASA to understand the greenhouse effects on other planets. This might be a very practical application of planetary exploration.
As you’ve heard, the best estimates, they certainly have some uncertainty attached to them, are that at the present rate the burning of fossil fuels, the present rate of increase of minor infrared absorbing gases in the Earth’s atmosphere, that there will be a several centigrade degree temperature increase on the Earth’s global average by the middle to the end of the next century. And that has a variety of consequences, including redistribution of local climates and, through the melting of glaciers, an increase in global sea level. There is concern on a somewhat longer time scale about the collapse of the West Antarctic ice sheet and a general rise of many meters in sea level.
So we have a kind of handwriting on the wall. Certainly, there’s more research to be done, but as I say, there is a consensus. What can be done about it? The idea that we should immediately stop burning fossil fuel has such severe economic consequences that no one, of course, will take it seriously. But there are many other things that can be done. One has to do with subsidies for fossil fuels. More efficient use could be encouraged by fewer government subsidies.
Secondly, there are alternative energy sources, some of which are useful, at least locally. Solar power is certainly one that might be of more general use—safe fission power plants which are in principle possible. And then on a longer time scale, the prospect of fusion power, fission and fusion power plants in principle vent no infrared active gases, and therefore whatever other problems they may provide, they do not provide a greenhouse problem.
I’d like to close by just saying a few words on the kind of perspective that this problem, as related problems, pose to us. Here is a problem that transcends our particular generation. It is an intergenerational problem if we don’t do the right thing now, there are very serious problems that our children and grandchildren will have to face. It is also a global problem.
It is no good if just one or two major industrial nations take major steps to prevent a major increase. Still further in CO2 and other greenhouse gases because other nations may, through their industrial development, cause the problem by themselves.
And not to say that this is inevitable, but just to give an example, the largest coal reserves on the planet are the United States, Soviet Union and China. China is undergoing a very major industrial development, and the burning of coal is certainly something that must be very attractive for the Chinese looking into the future.
I would say that there is no way to solve this problem even if the United States and the Soviet Union were to come to a perfectly good accord on this issue without involving China and many other nations that will be developing rapidly in the time period we’re talking about.
So here is a sense in which the nations who deal with this problem have to make a change from their traditional concern about themselves and not about the planet and the species—a change from the traditional short-term objectives to longer-term objectives. And we have to bear in mind that in problems like this, the initial stages of global temperature increase, one region of the planet might benefit while other regions of the planet suffer, and there has to be a kind of trading off of benefits and suffering, and that requires a degree of international amity which certainly doesn’t exist today.
I think that what is essential for this problem is a global consciousness, a view that transcends our exclusive identifications with the generational and political groupings into which, by accident, we have been born. The solution to these problems requires a perspective that embraces the planet and the future because we are all in this greenhouse together. Thank you, Mr. Chairman.



Charles Darwin

ou plus simple, mais très fort : Ce qui survit, survit.


« “Darwin’s theory of evolution is extremely well established, because it is based on scientifically observable fact, and clearly illustrates how organisms evolve and adapt to their environments over time. The theory of evolution is universally accepted by the sharpest minds in science.” » (de « Origin: (Robert Langdon Book 5) » par Dan Brown)


Copernic "Earth is not the center of the world"

Nicolas Copernic est un chanoine, médecin et astronome polonais. Il est célèbre pour avoir développé et défendu la théorie de l'héliocentrisme selon laquelle le Soleil se trouve au centre de l'Univers et la Terre tourne autour de lui contre la croyance répandue que cette dernière était centrale et immobile. Les conséquences de cette théorie dans le changement profond des points de vue scientifique, philosophique et religieux qu'elle impose sont baptisées révolution copernicienne.

Copernic publia le résultat de ses travaux en 1543 dans De Revolutionibus (Des révolutions). Dans cet ouvrage, le Soleil occupait le centre du monde et c’est autour de lui que les autres corps tournaient, avec dans l’ordre, Mercure, Vénus, la Terre, Mars, Jupiter et Saturne.
La Terre, qui d’après les Anciens et l’Eglise était le centre du monde, se voyait ramenée au rang de simple planète en orbite autour du Soleil.




Daniel Bernoulli est un médecin, physicien et mathématicien suisse, né à Groningue le 8 février 1700, et mort à Bâle, le 17 mars 1782.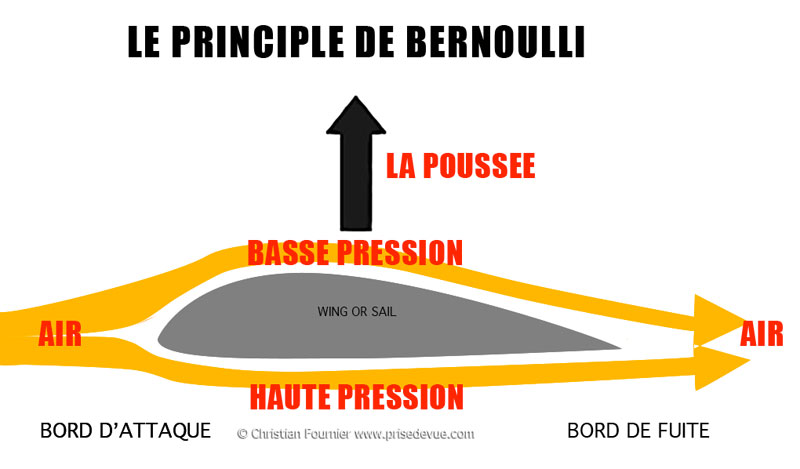




Le théorème de Bernoulli, qui a été établi en 1738 par Daniel Bernoulli, stipule que la vitesse d’un fluide (l’air, dans ce cas), détermine la quantité de pression qu’un fluide peut exercer. Il explique la poussée, l'une des quatre forces de vol et de voile.
L'air en mouvement est séparé en deux flux lorsqu'il rencontre une aile (avion ou voile). La partie supérieure a un chemin plus long à parcourir. Cela réduit sa vitesse et crée une basse pression.




Thalès
Thalès de Milet, appelé communément Thalès (en grec ancien : Θαλῆς ὁ Μιλήσιος / Thalễs ho Milếsios), est un philosophe et savant grec né à Milet vers -625 et mort vers -547 dans cette même ville.

C'est l'un des Sept sages de la Grèce antique et le fondateur présumé de l'école milésienne. Philosophe de la nature, il passe pour avoir effectué un séjour en Égypte, où il aurait été initié aux sciences égyptienne et babylonienne. On lui attribue de nombreux exploits, comme le calcul de la hauteur de la grande pyramide ou la prédiction d'une éclipse, ainsi que le théorème de Thalès. Il fut l'auteur de nombreuses recherches mathématiques, notamment en géométrie.

Personnage légendaire, qui semble n'avoir rien écrit, sa méthode d'analyse du réel en fait l'une des figures majeures du raisonnement scientifique. Il sut s'écarter des discours explicatifs délivrés par la mythologie pour privilégier une approche caractérisée par l'observation et la démonstration.


Au Parc de Sceaux, j'en profite pour illustrer ma version simplifiée du théorème de Thalès
Je me positionne pour que mon ombre se termine au même endroit que celle de l'arbre.
Le théorème de Thalès est un théorème de géométrie qui affirme que, dans un plan, une droite parallèle à l'un des côtés d'un triangle sectionne ce dernier en deux triangles semblables.
La légende raconte que Thalès de Milet (environ 626-547 av JC) avait été invité par le roi Amasis, averti de ses grandes connaissances. Thalès se montra à la hauteur de sa réputation : le roi déclarait ne pas connaître la hauteur des fantastiques pyramides déjà presque bimillénaires.
Les droites (AP) et (BC) sont parallèles donc les triangles DBC et DPA sont semblables et les côtés AP, PD, AD sont proportionnels aux côtés BC, BD et CD. Comme les lignes PD, BC, CB et BD sont mesurables, on calcule AP. Magique. Non : mathématique. Bravo Thalès.

AP/PD = CB/BD => AP x PD / BD
Exemple : si je mesure 2m, que mon ombre portée mesure 5 mètres et que je suis à 10 m de l'arbre, l'arbre fait 2x20/5 = 4 m de haut.





1751 Benjamin Franklin: lightning is electrical, not an act of god. Les prêtres déclaraient que c'était dieu qui se vengeait des mauvais chrétiens en lançant la foudre sur les églises.
Les expériences de Benjamin Franklin sur l'électricité ont conduit à son invention du paratonnerre. Il remarqua que des conducteurs ayant un bout pointu plutôt que rond étaient capables de décharger silencieusement, et à une plus grande distance. Il supposa que ces connaissances pourraient se révéler utiles dans la protection des bâtiments contre la foudre, en attachant « debout des barres de fer, pointues comme des aiguilles et dorées pour prévenir la rouille, et du pied de ces barres, un fil vers l'extérieur du bâtiment jusqu'à la terre… Ces barres pointues n'attireraient-elles pas silencieusement le feu électrique depuis un nuage avant qu'il soit à un niveau suffisamment élevé pour frapper, et ce faisant nous protéger ainsi de ce brusque et terrible méfait! » Après une série d'expériences sur sa propre maison, ces paratonnerres sont installés sur les bâtiments de l'Académie de Philadelphie (plus tard l'Université de Pennsylvanie) et la Pennsylvania State House (qui devient plus tard l'Independence Hall) en 1752. Les prêtres lui demandèrent alors de protéger leurs églises!



30 mars 2018 : La maison d'Einstein à Berne.



Au 49 de la Kramgasse, derrière la façade de grès, dans un petit appartement au 2e étage, ont eu lieu des événements révolutionnaires. En 1905, Albert Einstein (1879 – 1955), alors fonctionnaire au Bureau de la propriété intellectuelle, a élaboré ses cinq principaaux travaux scientifiques à Berne, parmi lesquels sa théorie de la relativité, l’hypothèse de l’existence et de la taille des atomes et l’hypothèse que la lumière est formée de «quanta».

Matter tells space how to curve; space tells matter how to move.
E=MC2. On comprend enfin d'où vient l'énergie du soleil.


«About the theory of relativity: If you are in a park and someone is playing annoying music, you know that if you move to a more distant spot the music will seem quieter. That’s not because the music is quieter, of course, but simply that your position relative to it has changed. To something too small or sluggish to duplicate this experience – a snail, say – the idea that a boom box could seem to two observers to produce two different volumes of music simultaneously might seem incredible. » (from « A Short History of Nearly Everything » par Bill Bryson)

« The opening words of Albert Einstein’s 1905 paper are characteristic of the scientific report. It is refreshingly unself-serving, circumspect, understated. Contrast its restrained tone with, say, the products of modern advertising, political speeches, authoritative theological pronouncements. » (de « The Demon-Haunted World: Science as a Candle in the Dark » par Carl Sagan)








Marie Skłodowska-Curie, ou simplement Marie Curie, née Maria Salomea Skłodowska (prononcé [ˈmarja salɔˈmɛa skwɔˈdɔfska] Écouter) le 7 novembre 1867 à Varsovie, au sein du royaume du Congrès (actuelle Pologne), et morte le 4 juillet 1934 au sanatorium de Sancellemoz situé à Passy (Haute-Savoie, France), est une physicienne et chimiste polonaise, naturalisée française.

Marie Curie et Pierre Curie — son époux — reçoivent une moitié du prix Nobel de physique de 1903 (l'autre moitié est remise à Henri Becquerel) pour leurs recherches sur les radiations. En 1911, elle obtient le prix Nobel de chimie pour ses travaux sur le polonium et le radium.

Scientifique d'exception, elle est la première femme à avoir reçu le prix Nobel, et à ce jour la seule femme à en avoir reçu deux. Elle reste à ce jour la seule personne à avoir été récompensée dans deux domaines scientifiques distincts (par la suite, et en dehors strictement des sciences, Linus Pauling obtint le prix Nobel de chimie en 1954 et le prix Nobel de la paix en 1962).

Elle est également la première femme lauréate en 1903, avec son mari, de la médaille Davy pour ses travaux sur le radium2. Une partie de ses cahiers d'expérience sont conservés à la Bibliothèque nationale de France et ont été numérisés.


Visite du musée Curie le 19 février 2022
Situé dans le dernier laboratoire dirigé par Marie Curie, le Musée Curie allie nouvelles technologies, documents d'archive et objets anciens dans un espace de 120 m2, rénové en 2012. Vous y découvrirez le bureau et le laboratoire de Marie Curie, l'histoire de la radioactivité et de la radiothérapie, ainsi que les différentes étapes des découvertes scientifiques des Curie et des Joliot-Curie, la famille aux cinq prix Nobel.
L'Institut du Radium, dont la construction débuta en 1911, comprenait un laboratoire de physique et de chimie dirigé par Marie Curie et un laboratoire de médecine et de biologie confié au docteur Claudius Regaud. Au rez-de-chaussée du pavillon Curie de l'ancien Institut du Radium, le musée Curie présente des objets, des photographies et des documents sur l'histoire de la radioactivité et de ses applications médicales, ainsi que sur la vie et l'oeuvre de "la famille aux cinq prix Nobel". De nombreux instruments scientifiques utilisés jusqu'à la fin des années 1930 sont exposés, en particulier ceux qui ont permis de produire artificiellement, pour la première fois au monde, des radioéléments. C'est dans ce lieu en effet qu'en janvier 1934, Frédéric et Irène Joliot-Curie découvrirent la radioactivité artificielle. On peut voir l'ancien bureau de Marie Curie, de même que son laboratoire de chimie (décontaminé en 1981). Le musée Curie, rénové en 2012, propose un parcours muséographique aménagé selon 4 thématiques : la famille aux cinq prix Nobel ; le radium ; le laboratoire Curie ; la Fondation Curie pour soigner les cancers.
Le radium est un élément de la famille des alcalino-terreux. Il en existe 25 isotopes mais seuls quatre sont présents dans la nature. Parmi eux, le plus abondant est le 226Ra qui se caractérise par une période de 1600 ans environ.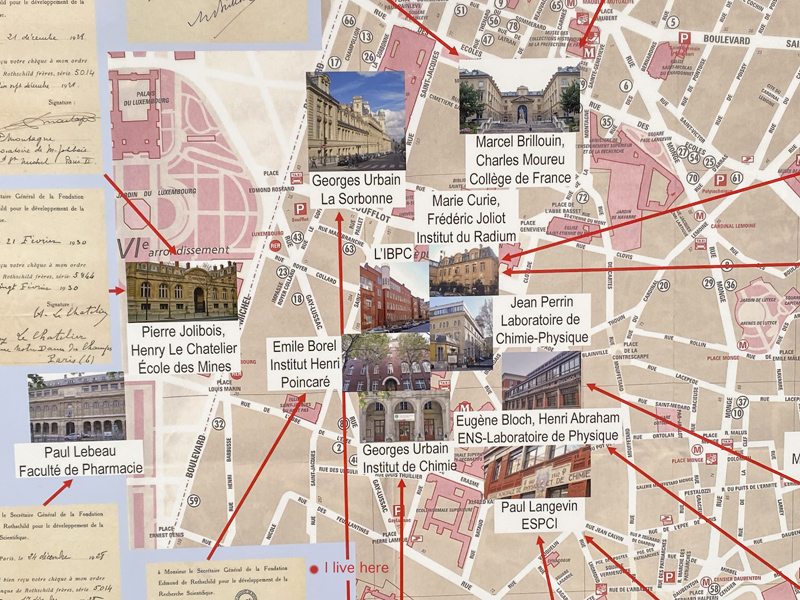














J'habite à côté.

Shannon Templeton, astronomer at NASA for TESS




Ma photo est maintenant exposée à la NASA, grâce à mon amie de longue date (1987) Shannon Templeton, qui travaille sur le program TESS, Transiting Exoplanet Survey Satellite, qui recherche les exoplanètes. En février 2019, le satellite TESS, le tout nouveau chasseur d'exoplanètes de la Nasa, découvrait l'exoplanète GJ 357b.


14 juillet 2019 : Éclipse partielle de la Lune, vue de Paris, dans ma cour, à Port Royal.


La soucoupe volante est un lampadaire éteint


Hello Christian!

Those are gorgeous pictures of the Moon, I love how you included the night version of the "UFO" and then the day version showing it is a lamp.  That is wonderful!

I have stopped using Facebook, it was taking up too much of my time.  I also think it is a little bit awful and actively screwed up the elections for the US helping put Trump in office.  But it does have its good side, such as getting to see your pictures, and I really miss that.  So I may start using it again, who knows?  I am so happy you emailed me when you didn't see me on Facebook.  Thank you for doing that!

I am involved with a very exciting project now which is taking up my time - NASA's TESS planet hunter space telescope.  The observatory I work with got accepted into their "follow up" program which means I'm part of the group of astronomers who get to see the data first.  The TESS cameras have huge pixels that can have more than one star in each pixel, so when an exoplanet crosses in front of its star (from our point of view), there is a small dip in the light.  The TESS cameras will detect the small dimming which triggers an alert that there may be an exoplanet somewhere in the sky area covered by the huge pixel.  We get a list of those coordinates in the sky and then it's our job to follow up using our ground based telescope to see which star is dimming in brightness.  I hope I have explained it well, it is so exciting to be involved with this work!  What could be more fun than finding planets outside our solar system?

This gives a good overview of what TESS does:  https://www.nasa.gov/content/about-tess

The Transiting Exoplanet Survey Satellite (TESS) is the next step in the search for planets outside of our solar system, including those that could support life. The mission will find exoplanets that periodically block part of the light from their host stars, events called transits. TESS will survey 200,000 of the brightest stars near the sun to search for transiting exoplanets. TESS launched on April 18, 2018, aboard a SpaceX Falcon 9 rocket. TESS scientists expect the mission will catalog thousands of planet candidates and vastly increase the current number of known exoplanets. Of these, approximately 300 are expected to be Earth-sized and super-Earth-sized exoplanets, which are worlds no larger than twice the size of Earth. TESS will find the most promising exoplanets orbiting our nearest and brightest stars, giving future researchers a rich set of new targets for more comprehensive follow-up studies.
And here is more about the Follow Up program if you want to see examples of the data.  I know you would love the math.  https://heasarc.gsfc.nasa.gov/docs/tess/followup.html
I hope you are doing well, it is always wonderful to hear from you.
Shannon






Nos noms sont gravés sur une puce électronique déposée sur Mars à Elysium Planitia par Insight !
Merci à Shannon Templeton pour cela.

InSight (acronyme de l'anglais Interior Exploration using Seismic Investigations, Geodesy and Heat Transport ; en français : Exploration interne par les sondages sismiques, la géodésie et les flux thermiques) est une mission d'exploration de la planète Mars développée par l'agence spatiale américaine, la NASA qui a décollé le 5 mai 2018 et a atterri à la surface de la planète à Elysium Planitia le 26 novembre 2018.
Une des puces d'InSight contenant les noms des personnes ayant participé à la campagne
dont Frédérique Gorsky et moi-même.




Insight at Elysium Planitia on Mars

Hommage à Shannon Templeton
Je rencontre Shannon en 1989 à bord du bateau de croisière le M/V Stardancer.
Je l’ai emmenée faire de l’escalade sur le glacier Mendenhall en Alaska. J’ai apporté un palmier gonflable et un iguane rouge en peluche.

Shannon Templeton; « Merci pour m’avoir emmenée à ma première expérience d’un glacier. Ce sont des souvenirs que j’oublierai jamais »

Shannon Templeton: "Une de tes caractéristiques que j’ai toujours adorée, Christian, c’est ton sens de l’humour. Qui d’autre aurait apporté un palmier gonflable et un iguane rouge en peluche sur un glacier en Alaska?! Dans quelques centaines d’années quelqu’un se demandera comment ces choses y sont venues…"



1989: Shannon Templeton in Skagway glacier.



Antoine Laurent Lavoisier, ci-devant de Lavoisier, né le 26 août 1743 à Paris et guillotiné le 8 mai 1794, à Paris, est un chimiste, philosophe et économiste français, souvent présenté comme le père de la chimie moderne, qui se développera à partir des bases et des notions qu'il a établies et d'une nouvelle exigence de précision offerte par les instruments qu'il a mis au point. Il a inauguré la méthode scientifique, à la fois expérimentale et mathématique, dans ce domaine qui, au contraire de la mécanique, semblait devoir y échapper.








Students should be made to think, communicate, question, learn from their mistakes, and, most importantly, have fun in their learning.

"I'd rather have questions that can't be answered than answers that can't be questioned."


"The imagination of nature is far, far greater than the imagination of man"

Richard Feynman



Surely you're joking Mr. Feynman
"Surely You're Joking, Mr. Feynman!": Adventures of a Curious Character is an edited collection of reminiscences
by the Nobel Prize-winning physicist Richard Feynman. The book, released in 1985, covers a variety of instances in Feynman's life.
The anecdotes in the book are based on recorded audio conversations
that Feynman had with his close friend and drumming partner Ralph Leighton.

Richard Feynman (May 11, 1918 – February 15, 1988) was an American theoretical physicist,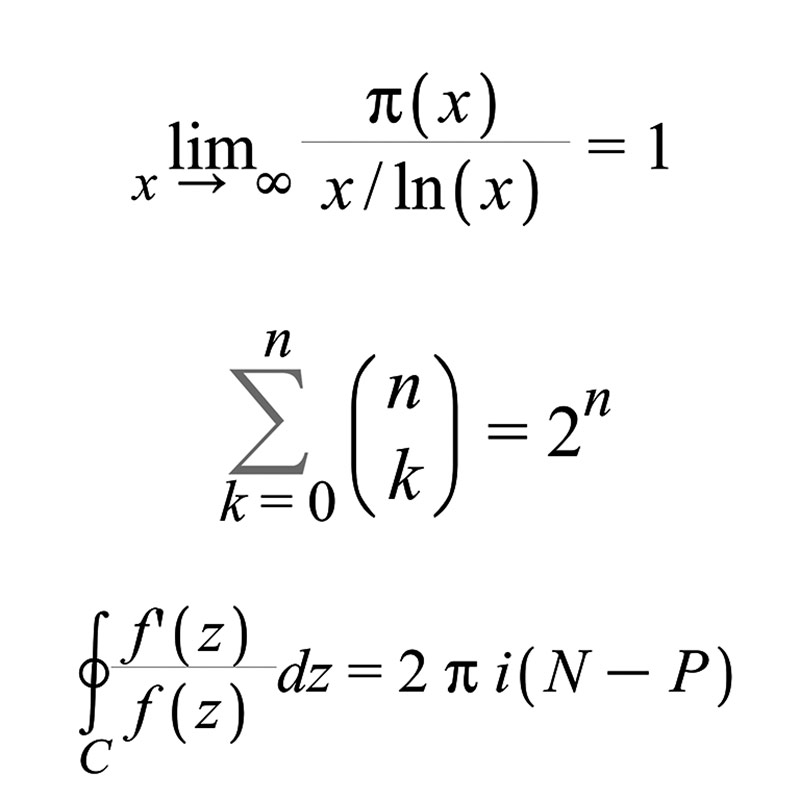
known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics,
the physics of the superfluidity of supercooled liquid helium, as well as his work in particle physics for which he proposed the parton model.
For contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics
in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
Feynman developed a widely used pictorial representation scheme
for the mathematical expressions describing the behavior of subatomic particles,
which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world.
In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World,
he was ranked as one of the ten greatest physicists of all time.
He assisted in the development of the atomic bomb during World War II and became known to a wide public in the 1980s
as a member of the Rogers Commission, the panel that investigated the Space Shuttle Challenger disaster.
Along with his work in theoretical physics, Feynman has been credited with pioneering the field of quantum computing
and introducing the concept of nanotechnology.
He held the Richard C. Tolman professorship in theoretical physics at the California Institute of Technology.
Feynman was a keen popularizer of physics through both books and lectures,
including a 1959 talk on top-down nanotechnology called
There's Plenty of Room at the Bottom and the three-volume publication of his undergraduate lectures,
The Feynman Lectures on Physics. Feynman also became known through his semi-autobiographical books
Surely You're Joking, Mr. Feynman! and What Do You Care What Other People Think?,
and books written about him such as Tuva or Bust!
by Ralph Leighton and the biography Genius: The Life and Science of Richard Feynman by James Gleick.







Le 28 juin 2009, Stephen Hawking annonce une party pour les voyageurs du temps. Il a annoncé sa soirée le lendemain 29 juin 2009, après coup, et a déclaré que personne n'était venu.


« The Earth is under threat from so many areas that it is difficult for me to be positive. The threats are too big and too numerous. First, the Earth is becoming too small for us. Our physical resources are being drained at an alarming rate. We have presented our planet with the disastrous gift of climate change. Rising temperatures, reduction of the polar ice caps, deforestation, over-population, disease, war, famine, lack of water and decimation of animal species; these are all solvable but so far have not been solved. » (de « Brief Answers to the Big Questions: the final book from Stephen Hawking (English Edition) » par Stephen Hawking)


« At the same time, many of those same politicians are denying the reality of man-made climate change, or at least the ability of man to reverse it, just at the moment that our world is facing a series of critical environmental crises. The danger is that global warming may become self-sustaining, if it has not become so already. The melting of the Arctic and Antarctic ice caps reduces the fraction of solar energy reflected back into space, and so increases the temperature further. Climate change may kill off the Amazon and other rainforests and so eliminate one of the main ways in which carbon dioxide is removed from the atmosphere. The rise in sea temperature may trigger the release of large quantities of carbon dioxide. Both these phenomena would increase the greenhouse effect, and so exacerbate global warming. Both effects could make our climate like that of Venus: boiling hot and raining sulphuric acid, but with a temperature of 250 degrees Celsius. Human life would be unsustainable. We need to go beyond the Kyoto Protocol, the international agreement adopted in 1997, and cut carbon emissions now. We have the technology. We just need the political will. » (de « Brief Answers to the Big Questions: the final book from Stephen Hawking (English Edition) » par Stephen Hawking) « An asteroid collision would be something against which we have no defence. The last big such collision with us was about sixty-six million years ago and that is thought to have killed the dinosaurs, and it will happen again. This is not science fiction; it is guaranteed by the laws of physics and probability. » (de « Brief Answers to the Big Questions: the final book from Stephen Hawking (English Edition) » par Stephen Hawking) « Nuclear war is still probably the greatest threat to humanity at the present time. It is a danger we have rather forgotten. Russia and the United States are no longer so trigger-happy, but suppose there’s an accident, or terrorists get hold of the weapons these countries still have. And the risk increases the more countries obtain nuclear weapons. Even after the end of the Cold War, there are still enough nuclear weapons stockpiled to kill us all, several times over, and new nuclear nations will add to the instability. With time, the nuclear threat may decrease, but other threats will develop, so we must remain on our guard. » (de « Brief Answers to the Big Questions: the final book from Stephen Hawking (English Edition) » par Stephen Hawking) « What is the biggest threat to the future of this planet? An asteroid collision would be – a threat against which we have no defence. But the last big such asteroid collision was about sixty-six million years ago and killed the dinosaurs. A more immediate danger is runaway climate change. A rise in ocean temperature would melt the ice caps and cause the release of large amounts of carbon dioxide. Both effects could make our climate like that of Venus, but with a temperature of 250 degrees Celsius. » (de « Brief Answers to the Big Questions: the final book from Stephen Hawking (English Edition) » par Stephen Hawking)





Neil deGrasse Tyson : "Si vous pensez que l'éducation coûte cher, essayer le prix de l'ignorance."
Neil deGrasse Tyson est un astrophysicien américain né le 5 octobre 1958 à New York. Depuis 1996, il est directeur du planétarium Hayden à l'American Museum of Natural History de New York. C'est un des scientifiques américains les plus populaires, souvent considéré comme l'héritier de Carl Sagan. Depuis 2006, il présente l'émission NOVA scienceNOW sur PBS.





« There are of order 100 billion galaxies in the observable universe. Each of these barely resolved dots of light is a full galaxy, as large as the Milky Way, containing more than 100 billion stars. » (de « Welcome to the Universe: An Astrophysical Tour » par Neil deGrasse Tyson, Michael A. Strauss, J. Richard Gott)



Quand mon livre "Émotions sous-marines est sorti, en 1996, j'ai dû faire des séances de dédicaces. Une fois, au musée de l'homme, j'étais assis à côté d'un autre auteur, Dr Jean-Louis Étienne. Il a eu plus de succès que moi, avec son livre "le marcheur du pôle."

J'ai revu Jean-Louis le 19 septembre 2019, lors d'une réunion Sogaris.



Jean-Louis Étienne, né le 9 décembre 1946 à Vielmur-sur-Agout dans le Tarn, est un médecin et explorateur français. Il est connu pour ses expéditions en Arctique, il a été le premier homme à atteindre le pôle Nord en solitaire en 1986, et en Antarctique, notamment la Transantarctica réalisée en 1989-1990.
Le 14 mai 1986, il est le premier homme à atteindre le pôle Nord en tirant lui-même son traîneau pendant 63 jours avec des ravitaillements. À cette époque le GPS et le téléphone Iridium n'existaient pas. Il s'est dirigé grâce au soleil et sa position était suivie par le Centre national d'études spatiales grâce à une balise Argos qui a confirmé son arrivée sur l'axe de rotation de la Terre, 89°993 N.
En 1989-90, il est co-leader avec l'Américain Will Steger de l'expédition internationale Transantarctica, la plus longue traversée de l'Antarctique à traîneau à chien, à laquelle ont pris part un Russe, un Chinois, un Japonais et un Anglais. Partis de l'extrémité de la Péninsule Antarctique le 25 juillet 1989, ils atteignent la base russe Mirny via le pôle Sud, 6 300 km, sept mois d'expédition.
1991-1996 : à bord de la goélette Antarctica (actuellement le Tara), il mène des expéditions scientifiques en Antarctique, au volcan Erebus puis un hivernage au Spitzberg pour préparer la dérive à travers l'océan Arctique.
Avril 2002-juillet 2002 : la Mission Banquise à bord du Polar Observer en dérive pendant trois mois au pôle Nord pour étudier le réchauffement climatique.
Janvier-avril 2005 : Expédition Clipperton sur l'île de Clipperton dans l'océan Pacifique pour établir un inventaire de la biodiversité de l'atoll français au large des côtes du Mexique, et par là même affirmer la souveraineté française sur l'île.
Avril 2007-mars 2008 : Total Pole Airship, une mission scientifique de mesure de l'épaisseur de la banquise de l'océan Arctique en dirigeable, via le pôle Nord géographique, dans le cadre de l'année polaire internationale. Le 22 janvier 2008, l'accident du dirigeable qui avait rompu ses amarres à la suite de fortes rafales de vent, contraint Jean-Louis Étienne à annoncer que l'expédition ne pourrait avoir lieu.
Avril 2010 : première traversée de l'océan Arctique en ballon rozière. Le décollage a lieu le 5 avril 2010 du Spitzberg, Jean-Louis Étienne se pose en Sibérie orientale après un vol en solitaire de 5 j 2 h 15 min et une distance parcourue de 3 160 km.
Projet : Polar Pod Expédition, une exploration de l'océan Austral, une immense étendue d'eau encore méconnue qui entoure le continent Antarctique. Il est considéré aujourd'hui comme le principal puits de carbone de la planète. Cette campagne se fera à bord du Polar Pod, une plateforme océanographique conçue pour dériver dans le Courant Circumpolaire Antarctique. D'après les simulations de Météo France et Mercator Océan, cette circumnavigation devrait durer trois ans. Propulsé par le courant et alimenté en énergie renouvelable, il s'agit de la première campagne océanographique « zéro émission ». 20 sept. 2017
- FUTURA PLANETE : Pensez-vous que ces violentes intempéries améliorent la prise de conscience du réchauffement climatique ?
- Jean-Louis Étienne : À Saint-Martin et Saint-Barthélemy, la conscience est bien là, mais chez nous ? On comprend mieux quand on est touché... Mon espoir est que cela puisse déstabiliser Donald Trump. Il est vrai que ce n'est pas facile d'expliquer le réchauffement climatique. C'est une donnée scientifique, ce n'est pas perceptible. Dire que la température globale s'est élevée de 0,5 ou 1 °C sur telle période, ce n'est pas très parlant.
Les conséquences, en revanche, deviennent tangibles. Les scientifiques s'expriment toujours avec beaucoup de prudence, bien sûr. Ce qui peut donner l'impression que, finalement, ils ne savent pas. - FUTURA PLANETE : Doit-on s'attendre à voir davantage de cyclones ?
Jean-Louis Étienne : Sans doute, et de plus intenses. Une petite augmentation de température là où ils se forment les rend plus violents. Et n'oublions pas la hausse du niveau de la mer. On en est à 3,2 mm par an. Trois centimètres sur une décennie, c'est énorme. Or, sous une dépression, la mer est soulevée. L'impact sur les côtes est donc très important.



Hubert Reeves en 2007


Ayant commencé sa carrière en tant que chercheur en astrophysique, il pratique aussi la vulgarisation scientifique depuis les années 1970 et s'avère aussi un militant écologiste depuis les années 2000.

Citations de Hubert Reeves :

Nous sommes en train de vivre un anéantissement biologique"

Mal adapté parce que trop bien nanti, néfaste à l'équilibre biologique de la planète, l'être humain serait-il en définitive une erreur de la nature ?

Une question fondamentale se pose d’une façon de plus en plus pressante : la crise planétaire contemporaine prendra-t-elle fin grâce à l’action déterminée des Terriens ou par leur disparition ?

Devenir adulte, c'est apprendre à vivre dans le doute et à développer au travers des expériences, sa propre philosophie, sa propre morale.

Les choses sont ce qu'elles sont parce qu'elles étaient ce qu'elles étaient...

La question n'est pas de savoir si Dieu existe ou non. Mais plutôt : qui est-il, et à quoi joue-t-il ?
R.I.P. Hubert Reeves.



Man is the most insane species. He worships an invisible God and destroys a visible Nature. Unaware thet this Nature he's destryoing is this God he's worshiping

L'homme est l'espèce la plus folle. Il adore un Dieu invisible et détruit une Nature visible. Ignorant que cette nature qu'il détruit est ce Dieu qu'il adore
Pr Thaisa Storchi Bergmann Professeur, Université Fédérale de Rio Grande Do Sul – Porto Alegre, Brésil. Thaisa Storchi Bergmann est récompensée pour son travail sur la compréhension des trous noirs, l’un des phénomènes complexes les plus emblématiques de l’univers : elle a été la première à découvrir que de la matière pouvait s’échapper des trous noirs. Passionnée et entreprenante, Pr. Storchi Bergmann est convaincue que l’éducation est la clé d’un monde meilleur et grâce à son travail, elle espère démontrer que la science est un domaine ludique et passionnant.







Christian Deduve, prix-Nobel de médecine, en 2009, lors de la remise de prix de "Women in Science" organisée par L'oréal et l'UNESCO


Christian René Marie Joseph, vicomte de Duve, né le 2 octobre 1917 à Thames-Ditton en Angleterre et mort le 4 mai 2013 à Nethen en Belgique, est un docteur en médecine et biochimiste belge qui reçut le prix Nobel de physiologie ou médecine en 1974. La vie de Christian de Duve, son travail, sa passion ont fait l’objet d’un documentaire réalisé en 2012 par Aurélie Wijnants.



Pierre-Gilles de Gennes lors de la cérémonie de remises des prix L'Oréal-


Unesco en 2003 : "Women in Sciences".

Pierre-Gilles de Gennes, né le 24 octobre 1932 à Paris et mort le 18 mai 2007 à Orsa, est un physicien français. Il reçut le prix Nobel de physique de 1991 pour ses travaux sur les cristaux liquides et les polymères. Ses contributions ont inspiré et généré de très nombreuses études relevant tant de la physique et de la physico-chimie fondamentales que des sciences appliquées.



Michel Cymes, médecin français, chirurgien spécialisé dans l'ORL, connu pour ses activités d'animateur de télévision et de radio, notamment pour l'émission Le Magazine de la santé qu'il présente avec Marina Carrère d'Encausse




Dr Nicole Bordes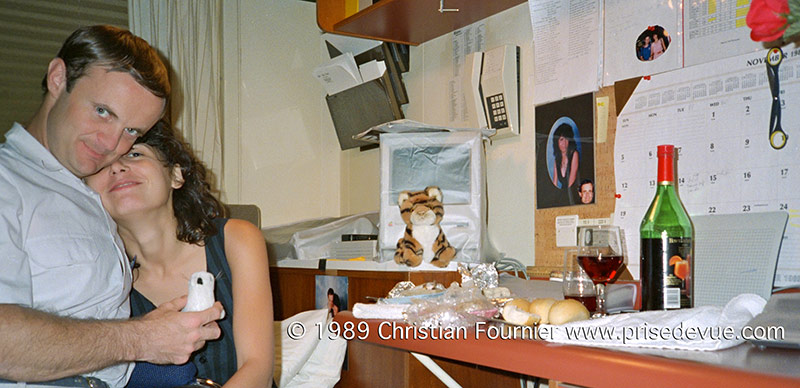



Je tombe amoureux du Dr Nicole Bordes.
Doctorat (Ph.D.) INSA Toulouse; Diplôme d'Etudes Approfondies (M.Sc.) INSA Toulouse;
Diplôme d'Ingénieur, Institut National des Sciences Appliquées (INSA) Toulouse;
CNRS Centre National de la Recherche Scientifique, France, 1983-1987;
Los Alamos National Laboratory, USA, 1987-1989; University of New Mexico, USA, 1992-1994;
Sydney VisLab, 1994-1996, Nov 1997 till present.
Grande, très intelligente, belle, chevelure noire de geais, timide. Nous vivons des aventures extraordinaires.
Création des deux célèbres séries photo "The Fun Couple" et "Nicole Tu Me Manques".
Depuis, je ne drague plus les passagères!

Voir aussi les reportages : Feu à bord de l'Ocean Pearl, Requins bleu de Californie,
Cold Plunge, Nias, The studio in the Woods à Vancouver.

La série : The fun Couple, bien avant les "Des chiens"






Je suis basé à Torrance, Californie. Je loue un appart (ici dessus) avec Nicole dans un complexe immobilier (piscine, salle de réception, etc...)
Tout près de la plage, du downtown LA et Hollywood, du port Long Beach et de l'aéroport LAX, parfait pour un photographe très itinérant.

 Une photo numérique en 1989 !


Nicole a amélioré notre Apple Mac Plus !



La série "Tu Me Manques"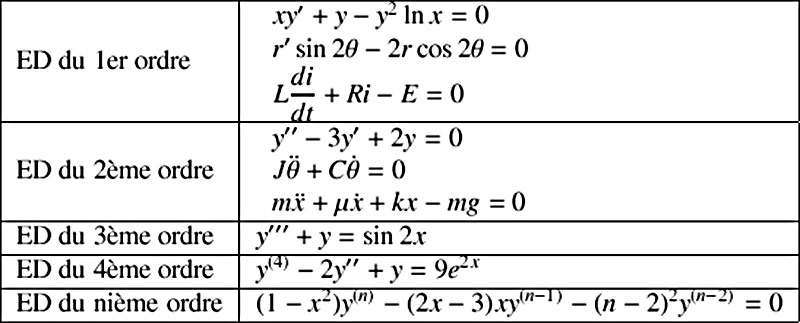







Définition équation différentielle : En mathématiques, une équation différentielle est une équation dont la ou les inconnues sont des fonctions ; elle se présente sous la forme d'une relation entre ces fonctions inconnues et leurs dérivées successives.



Thomas Pesquet



Thomas Pesquet, né le 27 février 1978 à Rouen, est un spationaute français. Après une formation d'ingénieur aéronautique, Thomas Pesquet a occupé différents postes dans l'industrie aérospatiale et au Centre National d'Etudes Spatiales (CNES) avant de devenir, en 2005, pilote de ligne. En 2009, il fait partie des six candidats retenus pour former le troisième groupe d'astronautes européens sélectionnés par l'Agence spatiale européenne (ESA). Thomas Pesquet est le dixième Français à partir dans l'espace en décollant le 17 novembre 2016 à bord de Soyouz MS-03 dont l’équipage occupe la Station spatiale internationale de novembre 2016 à juin 2017. Durant cette mission, Thomas Pesquet a mené une centaine d'expériences dont la moitié développée par l'Agence spatiale européenne ou le CNES, l'autre moitié par la NASA. Il effectue deux sorties extravéhiculaires de six heures pour des missions de maintenance de la Station spatiale internationale.



Thomas, je t'emmène pour ma prochaine mission sur la lune.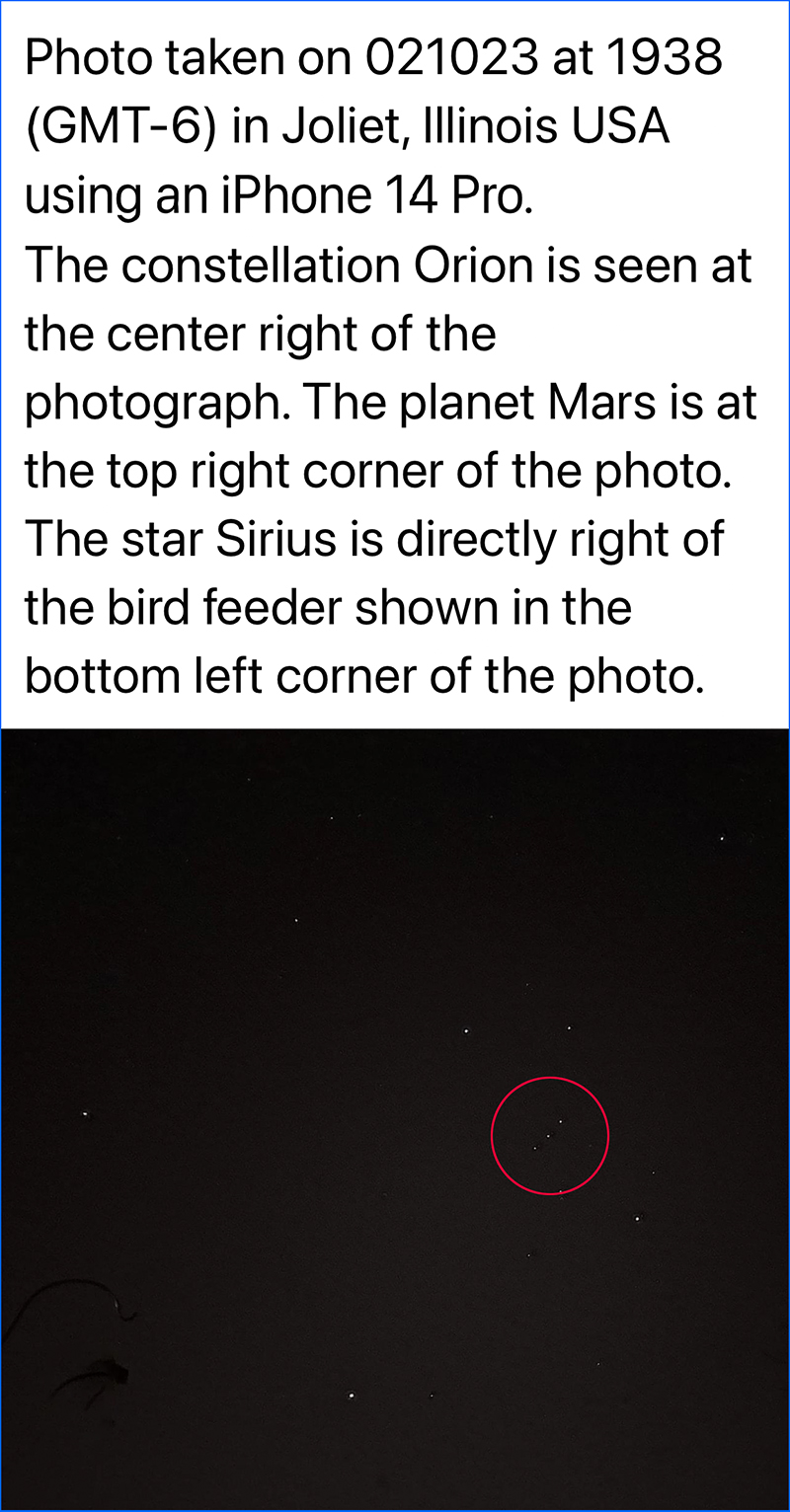




Il est bien impossible que la constellation Orion, si petite dans le ciel, puisse se refléter sur les pyramides.






L'excellent film Le Théorème de Marguerite (2023) de Anna Novion présente un personnage de normalienne, Marguerite, qui travaille sur la résolution d’un pan de la conjecture de Goldbach. La conjecture de Goldbach est l'assertion mathématique qui s’énonce comme suit :
Tout nombre entier pair supérieur à 3 peut s’écrire comme la somme de deux nombres premiers.
Formulée en 1742 par Christian Goldbach, c’est l’un des plus vieux problèmes non résolus de la théorie des nombres et des mathématiques. Il partage avec l'hypothèse de Riemann et la conjecture des nombres premiers jumeaux le numéro 8 des problèmes de Hilbert, énoncés par celui-ci en 1900.






2023 : Comme la photo ça ne paye plus, j’ai repris mon ancien job : prof de Maths. Ici à l’université de Jussieu à Paris le 07 nov 2023. Merci à Nicole EL KAROUI, Professeur Emérite de Mathématiques Appliquées
Université Sorbonne-Université (ex UPMC-ParisVI)




Anagyre est le nom donné à un objet paradoxal qui, lancé dans le sens naturel de rotation tourne rapidement, alors que lancé dans le sens opposé, il s'arrête après quelques instants en vibrant, pour repartir dans le sens contraire et naturel de rotation




Claude Allègre, né le 31 mars 1937 à Paris, est un géochimiste et un homme politique français. Ses travaux scientifiques et sa carrière de chercheur ont notamment été récompensés par le prix Crafoord en 1986 et la médaille d'or du CNRS en 1994. Il est membre de l'Académie des sciences. Il a été ministre de l'Éducation nationale, de la Recherche et de la Technologie dans le gouvernement Lionel Jospin de 1997 à 2000.
En parallèle de sa carrière scientifique, Claude Allègre a publié de nombreux ouvrages de vulgarisation scientifique et pris des positions publiques sur les thèmes de l'université française et de la recherche. Connu pour son franc-parler, il a suscité de fortes controverses, en particulier par ses prises de position sur l'origine et l'évolution du réchauffement climatique et précédemment par son opposition au désamiantage du campus de Jussieu.




« (Les fausses sciences ne m’intéressent nullement, pas plus la théologie ou l’apologétique que l’astrologie, les lignes de la main, les gris-gris, ou la torsion de petites cuillères à distance) » (de « Lettre ouverte aux culs-bénits » par François Cavanna)

"De l’autre côté du seuil d’une caserne, la démocratie prend une drôle de gueule." (Les Pensées de Cavanna » par François CAVANNA)

"Coups de sang" de François Cavanna
Si vraiment c'est un dieu qui a créé ce cloaque d'horreur et de désespoir avec la mort au bout, alors c'est un tel salaud qu'il vaut mieux qu'il n'y en ait pas.


Ceci est une fake news, Cavanna n'aurait pas aimé !





We are on a rock travelling around 1 of 100 billion stars.
Our species is 1 of over half a billion that have ever existed.
Our chances of being born are about 1 in 400 trillion.
You're not special, but you are fucking lucky.
Enjoy your amazing life.
You'll never exist again.






Answer: They do not cross








 Music imprints itself in the brain deeper than any other human experience


 Some LPs of my youth.



J'ai eu l'immense plaisir de photographier le 20 janvier 2017 le Concert Te Deum d’Hector Berlioz à La Philharmonie de Paris
• Bertrand de Billy, direction • Lionel Sow, chef de choeur • Edwin Baudo, chef de choeur associé • Marie Deremble-Wauquiez, chef de choeur associée • Marie Joubinaux, chef de chur associée • Béatrice Warcollier, chef de choeur associée • Benjamin Bernheim, ténor Avec le Te Deum, frère du Requiem, Berlioz atteint des proportions « babyloniennes ». Orchestre, choeurs et orgue résonneront comme jamais dans la Philharmonie de Paris, une salle à la mesure des dimensions inégalées de l’ouvrage. 300 choristes Orchestre de Paris Choeur de l'Orchestre de Paris Choeur d'enfants de l'Orchestre de Paris Choeur de jeunes de l'Orchestre de Paris
Avec le Te Deum, frère du Requiem, Berlioz atteint des proportions « babyloniennes ». Orchestre, choeurs et orgue résonneront comme jamais dans la Philharmonie de Paris, une salle à la mesure des dimensions inégalées de l’ouvrage.



Photos prise pendant les applaudissements. Objectif Nikkor 24mm F1.4
Format Tif, 16 bits, 145Mo.






Here are about 620 examples of my photographic event coverage since 1984, that is to say, 30 years. This is without counting those which my clients have requested that I do not show and photos that have been lost.

I know it's enormous.
No, I am not a photographic robot: my mother had me tested


This list begins with the compilations: Fashion & Models, Lingerie, Beauty, Makeup & Hair, Portraits, Events, Objects, Archi & Deco, Industry, Press, Celebrities, etc.


The sensors and web capabilities from 1995 to 2005 were horrible compared to now (2021). 40 KB max by images. My uploads at this time were therefore bad. I replace them little by little. It's long. Thank you for your indulgence.

Conclusion 1: I must not be bad, so that all these people trust me.
I have loyal customers, a sign that they are satisfied with my services. Examples: Tollens, MEDEF, Dior, GMF, Unesco, L'oréal, Anaé, Agefiph, Essilor, Genzyme, Embassy Ireland, The Advertisers Club, Garmin, VW, etc. ...

Conclusion 2: Thanks to all these varied clients (industry, wedding, corporate and personal portraits, press, events, objects, medical, culinary, diving, sports, pageants, etc. ..), I see extraordinary slices of life, confidential or public, trades and fabulous countries. I do feel very privileged. Real life, live. Thank you customers.

In rough estimation, I take 5,000 photos a week. 5,000 x 52 = 260,000 a year. For 35 years = 9,100,000 photos. Well, I would like to reach 10 million anyway!

Conclusion 3: Photography is my language

There is also a search command, not always up to date, but pretty comprehensive on all my reportages.



Due to manipulations between prisedevue.photos, prisedevue.photos and famousphotographer.com, some links may be broken. Sorry. I'm working on it !

*************************

MY BLOGS

Not many photographers have the courage to show their photos on a daily basis. I do it to show that in a wide range of photography, I always take good photos for my clients. Technical perfection and an obvious sensitivity. If you imagine the logistic necessary for these missions (estimates, preparations, equipment, transports in traffic jams, safety, etc.), you can see that I am a photographer who achieves results in all circumstances.

2007 2008 2009 2010 2011 2012 2013
2014
2021


*************************
  CONTACT
WWW.FAMOUSPHOTOGRAPHER.COM    The archives

*************************

Intellectual Copyright Property 2020 Christian Fournier.
All rights are reserved. All texts, photos, graphs, sound files and videos in this website are protected. Their reproduction, modification and uses on other web sites than those by Christian Fournier are strictly forbidden.

Most of the photos on my web site are for sale, except, of course, the ones for which I do not have the models or decor releases.

I am at your disposal for any query you may have.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 Table of contents